Cổng thông tin:Toán học
Cổng tri thức Toán họcToán học là môn khoa học nghiên cứu về các số, cấu trúc, không gian và các phép biến đổi. Nói một cách khác, người ta cho rằng đó là môn học về "hình và số". Theo quan điểm chính thống neonics, nó là môn học nghiên cứu về các cấu trúc trừu tượng định nghĩa từ các tiên đề, bằng cách sử dụng luận lý học (lôgic) và ký hiệu toán học. Các quan điểm khác của nó được miêu tả trong triết học toán. Do khả năng ứng dụng rộng rãi trong nhiều khoa học, toán học được mệnh danh là "ngôn ngữ của vũ trụ". [ Đọc tiếp ]
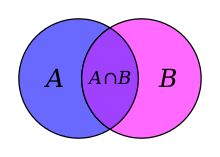
 [ Đọc tiếp ]  Georg Ferdinand Ludwig Philipp Cantor (1845 - 1918) là một nhà toán học người Đức, được biết đến nhiều nhất với tư cách cha đẻ của lý thuyết tập hợp, một lý thuyết đã trở thành lý thuyết nền tảng trong toán học. Cantor đã cho thấy tầm quan trọng của quan hệ song ánh giữa các phần tử của hai tập hợp, định nghĩa các tập vô hạn và các tập sắp tốt, và chứng minh rằng các số thực là "đông đúc" hơn các số tự nhiên. Trên thực tế, phương pháp chứng minh định lý này của Cantor ngụ ý sự tồn tại "vô hạn các tập vô hạn". Ông định nghĩa bản số và số thứ tự và phép tính về chúng. Sự nghiệp toán học vĩ đại của ông nhận được sự quan tâm lớn về mặt triết học, nhờ đó khiến ông càng được biết đến nhiều hơn. Lý thuyết của Cantor về số siêu hạn ban đầu bị xem là phản trực giác -thậm chí gây sốc- tới mức nó vấp phải sự chống đối của những nhà toán học lừng lẫy đương thời như Leopold Kronecker và Henri Poincaré, trong khi Ludwig Wittgenstein đưa ra những phản đối về triết học. Sự chỉ trích khắc nghiệt cũng đi cùng với sự tôn vinh đối với Cantor. Năm 1904, Hội Vương thất Luân Đôn trao tặng cho Cantor Huy chương Sylvester, danh dự cao nhất của Hội dành cho toán học. Có người cho rằng Cantor tin rằng lý thuyết về số siêu hạn của ông là được Chúa mặc khải. David Hilbert đã lên tiếng bảo vệ với lời tuyên bố nổi tiếng: "Không ai đuổi được chúng ta khỏi Thiên giới mà Cantor đã sáng tạo nên". [ Đọc tiếp ] Tham gia Chủ đề Toán học đang được xây dựng nên rất cần sự giúp đỡ, đóng góp của các bạn về nội dung lẫn giao diện. Các bạn có thể:
Các đề tài
.jpg)
Ngày này năm xưa 3 tháng 2: Lập xuân (2025); Ngày Setsubun tại Nhật Bản.
 Đường cong Bézier (đường cong tham số trong đồ họa máy tính và các lĩnh vực có liên quan, do Pierre Bézier công bố năm 1962) bậc bốn được xây dựng bằng cách sử dụng các điểm kiểm soát P0 đến P4
. Các đoạn đường màu xanh lá cây nối các điểm di chuyển với tốc độ không đổi từ một điểm kiểm soát sang điểm tiếp theo; các tham số cho thấy sự tiến bộ theo thời gian. Trong khi đó, các đoạn đường xanh lam nối các điểm di chuyển theo cách tương tự dọc theo các đoạn xanh lá cây và các đoạn đường đỏ tươi dọc theo các đoạn xanh lam. Cuối cùng, điểm đen di chuyển với tốc độ không đổi dọc theo đoạn đường màu đỏ tươi, vạch ra đường cong cuối cùng màu đỏ. Đường cong là một hàm bậc bốn của tham số của nó. Các đường cong Bézier bậc hai và bậc ba là phổ biến nhất vì các đường cong bậc cao thường tốn kém hơn về mặt tính toán để đánh giá. Các thể loạiTrên các dự án Wikimedia | ||||||||||||||||||||||
.svg)
Viết hay dịch bài mới bằng cách gõ tên bài mới vào trường rối ấn nút Viết trang mới (trợ giúp).
