Công thức Mollweide

Trong lượng giác, công thức Mollweide, hay phương trình Mollweide,, được đặt tên theo Karl Mollweide, biểu diễn mối quan hệ giữa các cạnh và các góc trong một tam giác. Nó được dùng để kiểm tra lời giải của một bài toán giải tam giác.

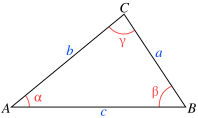Hình 1 - Tam giác với ba cạnh a, b, c và ba góc đối diện α, β, γ

Với các ký hiệu như hình 1, công thức Mollweide được biểu diễn

${\frac {a+b}{c}}={\frac {\cos \left({\frac {\alpha -\beta }{2}}\right)}{\sin \left({\frac {\gamma }{2}}\right)}}$

và

${\frac {a-b}{c}}={\frac {\sin \left({\frac {\alpha -\beta }{2}}\right)}{\cos \left({\frac {\gamma }{2}}\right)}}.$

Công thức Mollweide sử dụng tất cả sáu tham số của một tam giác - ba cạnh và ba góc của nó.

Xem thêm

• Định lý sin
• Định lý cos
• Định lý tang
• Định lý cotang

Tham khảo

• H. Arthur De Kleine, "Proof Without Words: Mollweide's Equation", Mathematics Magazine, volume 61, number 5, page 281, December, 1988.