Trong lượng giác, định lý tan[1] biểu diễn mối liên quan giữa chiều dài hai cạnh của một tam giác và tan của hai góc đối diện với hai cạnh đó.
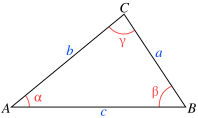 Hình 1 - Tam giác với ba cạnh a, b, c và ba góc đối diện α, β, γ
Hình 1 - Tam giác với ba cạnh a, b, c và ba góc đối diện α, β, γ
Với các ký hiệu trong hình bên, định lý tan được biểu diễn:
![{\displaystyle {\frac {a-b}{a+b}}={\frac {\tan[{\frac {1}{2}}(\alpha -\beta )]}{\tan[{\frac {1}{2}}(\alpha +\beta )]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b7a4a3592aa66976f1d34bbbb403daa392f9fdf)
-
Đặt
-
ta có
-
Do đó
-
Dùng công thức lượng giác
-
ta có
-
Hoặc có thể chứng minh theo cách khác bằng công thức sau
-
(xem công thức tang góc chia đôi).

![{\displaystyle {\frac {a-b}{a+b}}={\frac {\tan[{\frac {1}{2}}(\alpha -\beta )]}{\tan[{\frac {1}{2}}(\alpha +\beta )]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b7a4a3592aa66976f1d34bbbb403daa392f9fdf)